Current Loop Transformed for a Rotating Charge

Introduction

            In this animation we have a circular conducting loop of radius a with current running along its circumference.  Just adjacent and above the loop (by δz) we also have a charge Q that is moving in the tangential direction with angular speed w and at radius a.  We would like to transform both the fixed charges and the moving mobile charges in the loop so that the external charge is stationary.  This will cause the loop's magnetic forces on Q to become zero and be converted to electric forces of the same value and direction.

 

Loop Kinematics

            Before transformation charge $q_{test}$ has the coordinates

$$r_{qtest}(t)=a\widehat{x}\cos \omega t+a\widehat{y}\sin \omega t+\widehat{z}\delta z$$

(1.1)

Similarly the velocity of $q_{test}$ is:

$$v_{qtest}(t)=-\omega a\widehat{x}\sin \omega t+\omega a\widehat{y}\cos \omega t$$

(1.2)

To cause the rotation rate of the loop to make the velocity of $q_{test}$ look like it's zero we choose to give the loop a rotation rate of the opposite sign

$${\Omega }_{loop}=-{\omega }_{qtest}$$

(1.3)

Then a  fixed charge, $q_f$ , at initial angle $\varphi$ in the loop will have the coordinates

$$r_{q_f}(t,\varphi )=a\widehat{x}\cos (\Omega t+\varphi )+a\widehat{y}\sin (\Omega t+\varphi )$$

(1.4)

and its velocity will be

$$v_{q_f}(t,\varphi )=-\Omega a\widehat{x}\sin (\Omega t+\varphi )+\Omega a\widehat{y}\cos (\Omega t+\varphi )$$

(1.5)

Further, a mobile charge, q_m ,  at initial angle ψ, that contributes to the current by having a rotational rate of Ω_m with respect to the loop will have coordinates:

 

$$r_{q_m}(t,\varphi )=a\widehat{x}\cos [(\Omega +{\Omega }_m)t+\psi ]+a\widehat{y}\sin [(\Omega +{\Omega }_m)t+\psi ]$$

(1.6)

and this same charge will have velocity:

$$v_{q_m}(t,\varphi )=a(\Omega +{\Omega }_m)\{-\widehat{x}\sin [(\Omega +{\Omega }_m)t+\psi ]+\widehat{y}\cos [(\Omega +{\Omega }_m)t+\psi ]\}$$

(1.7)

 

Now let's assume that $\delta z$ is very small so that only the loop's charges that are very close to $q_{test}$ can cause significant force on $q_{test}$.  Also assume that the loop's counter-rotation started when t=0 so that the test charge was at coordinates (a,0). 

Then the loop charges that we have to be concerned with are going to be moving in the y direction.  Their spacing will be reduced by the factor $1/\gamma$ where $\gamma =1/\sqrt{1-{(v/c)}^2}$ and v is their speed in the y direction and can never exceed c.  For the fixed charges we have

$${\gamma }_f=1/\sqrt{1-{(\Omega a/c)}^2}$$

(1.8)

and for the mobile charges we have

$${\gamma }_f=1/\sqrt{1-{[(\Omega +{\Omega }_m)a/c]}^2}$$

(1.9)

An example of the these transformations is shown in Figure 1.

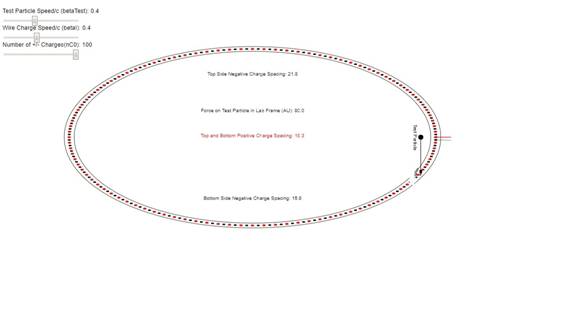
Figure 1: The transformed current loop as viewed by the (now) stationary test charge on its right hand side.  The charge spacings on the right and left side are closer than the spacings on the top and bottom. In the program this is achieved by simply scaling of the (x,y) dimension as (1,1/γ).

 

An expression for the electric field in the z direction due to a linear charge density, $\lambda$ , that extends in the y direction from $-ltol$ is

$$E_z=\frac{2l\lambda }{2\pi {\epsilon }_{0}z\sqrt{z^2+l^2}}$$

(1.10)

where (0,0,z) is the position of observation.  When $l>>z$ then equation (1.10) becomes

$$E_z=\frac{2\lambda }{2\pi {\epsilon }_{0}z}$$

(1.11)

            For relativistic speed there are two correction factors that must be applied to these electric field components.  First, $\lambda$ has to be corrected by multiplying by the appropriate $1/\gamma$ of equations (1.8) and (1.9).  Then, for E fields perpendicular  to the direction of charge flow, the electric field of each elemental charge is enhanced by the factor $\gamma$ http://www.feynmanlectures.caltech.edu/II_26.html.  It would seem that, for the stationary test particle, the forces in the z direction require no relativistic transformation since the two correction factors cancel.

 

We can't expect to cancel the current by rotating the loop oppositely to the direction of the test charge.  We will still have a net current ${\lambda }_I{v}_I$ so we will still have a magnetic field.  However, that magnetic field will not exert a force on the stationary test particle  since its speed is zero.  But we will have a net charge associated with the speed of the current since moving charges spacing is less than static charge spacing.

 

Lorentz Boosts of Added Velocities

We will need to have the factors $\gamma$ for the sum of the negative charge speed, ${\beta }_I$  and the rotational speed of the loop, ${\beta }_t$ where generically $\beta =v/c$ .

The addition equation for $\beta$ is

$$\beta {}_{IT}=\frac{{\beta }_I-{\beta }_t}{1-{\beta }_I{\beta }_t}$$

(1.13)

Then we can write

$$\frac{1}{{\gamma }_{IT}^2}=1-{\beta }_{IT}^2$$

(1.14)

We can re-write equation (1.14) as

                                                                                                                                       (1.15)

$$\frac{1}{{\left({\gamma }_{IT}^{}\right)}^2}=\frac{(1-{\beta }_I^2)(1-{\beta }_t^2)}{{\left(1-{\beta }_I{\beta }_t\right)}^2}$$

(1.16)

and re-naming some quantities using ${\gamma }_I=1/\sqrt{1-{\beta }_I^2}$ and ${\gamma }_t=1/\sqrt{1-{\beta }_t^2}$ we obtain

$${\gamma }_{IT}^2={\gamma }_I^2{\gamma }_t^2{(1-{\beta }_I{\beta }_t)}^2$$

(1.17)

It would at first seem that the linear charge density has to be multiplied by the factor:

$${\lambda }_I^{\text{'}}={\gamma }_I{\gamma }_t(1-{\beta }_I{\beta }_t){\lambda }_I$$

(1.18)

You should recall that the negative charge was moving prior to this transformation, and therefore charge spacings were contracted by $\frac{1}{{\gamma }_I}$ prior to this transformation.  Thus to get the effective negative charge density this value of ${\gamma }_{IT}$ must be divided by ${\gamma }_I$ so that the factor multiplying the negative  charge density is:

$${\lambda }_I\text{'}={\gamma }_t^{}(1-{\beta }_I{\beta }_t){\lambda }_I$$

(1.19)

Obviously the negative charge density in the parts of the loop that are not just adjacent to the test charge would be changed to compensate for those near the  test particle.

The total charge density near the test charge is the sum of the positive and negative charge densities

$$\lambda \text{'}={\lambda }_0[1-{\gamma }_t^{}(1-{\beta }_I{\beta }_t)]={\lambda }_0{\beta }_I{\beta }_t{\gamma }_t$$

(1.20)

 When the law for transformation of the force from the charge's moving frame to the laboratory frame

$$F_{testch\arg estationary}={\gamma }_t{F}_{moving}$$

(1.21)

is taken into account, the ${\gamma }_t$ factor in equation (1.20) is factored out and the new electric force is the same as the magnetic force before transformation.