Accelerated Space Trip Signal Reception Rates

Introduction

One of the "standard" graphics associated with accelerated space trips is to show a large group of evenly spaced signals sent by the inertial frame (earth) to the accelerated frame (rocket) and vice versa. That might be a worthwhile endeavor but it would be more interesting to see how the signal reception rates vary as the space trip continues since this will be some measure of apparent variation the clock rates. The present document will compute these reception rates.

Rocket to Earth Reception Rate

To be definite, our signals will be very short light pulses so we'll use the term pulse from now on.

We'll start with pulses sent from the rocket to earth. These will be sent at equal increments, $d t$ , of rocket proper time so their emission events will resemble the ticks of the rocket clock. The displacement at which emission occurs is the rocket displacement, $x_{r} (t)$ .

To compute $x_{r} (t)$ for a general acceleration program which has acceleration phases as well as cruise phases we will need the time integral of the acceleration

$θ (t) = \int_{0}^{t} a (t') d t'$

(1.1)

where a(t) is the acceleration as a function of rocket proper time.

Then we can obtain the emission displacement, $x_{r} (t_{i})$ , for the ith pulse, by the following integral

$x_{r} (t_{i}) = c \int_{0}^{t_{i}} t a n h θ (t') d t'$

(1.2)

The pulses proceed toward the earth at the speed of light which means that they travel upward in the Minkowski space time diagram (ct, x) and toward the earth world line at an angle of 45 degrees. Therefore at t', subsequent to emission, their coordinates will be:

$(c t_{i}^{'}, x_{i}^{'}) = [c t_{i}, x_{r} (t_{i})] + [c (t^{'} - t_{i}), - c (t^{'} - t_{i})]$

(1.3)

We need to compute the time of reception of the ith pulse at x=0. Obviously,

$c (t' - t_{i}) = x_{r} (t_{i})$

(1.4)

so that we have the difference between reception of the ith pulse and the (1+1)th pulse

$t'_{i + 1} - t'_{i} = t_{i + 1} - t_{i} + \frac{x_{r} (t_{i + 1}) - x_{r} (t_{i})}{c}$

(1.5)

We are now ready to compute the retarded rate of reception for a particular pulse. Note that:

$\frac{d}{d (t_{i})} x_{r} (t_{i}) = c \tanh θ (t_{i})$

(1.6)

and this will cause a difference between reception rate and emission rate. When tanh is positive this causes a decreasing rate of reception while when tanh is negative it causes an increasing rate of reception. It is the same as a Doppler shift in frequency but its effect is retarded by the value of x(t)/c.

Then the rate of reception, dn/dt, at time t' is:

$\frac{d n}{d t'} = \frac{d n}{d t} \sqrt{\frac{1 - \tanh [θ (t' - x (t_{i}) / c]}{1 + \tanh [θ (t' - x (t_{i}) / c]}}$

(1.7)

where dn/dt is the rocket's proper time rate of pulse emission.

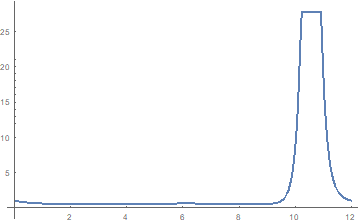
Figure 1: Plot of relative earth reception rate, dn/dt'/(dn/dt),equation (1.7), as a function of t for acceleration=1 light year/year² .

This completes the calculation of the rate of reception from the rocket to the earth.

Earth to Rocket Reception Rate

The rocket is moving with respect to the world line of the earth at speed $v_{r} (t) = c \tanh θ (t)$ and its distance at time t is

$x_{r} (t) = c \int_{0}^{t} t a n h θ (t') d t'$

(1.8)

The reception rate is Doppler shifted by the following factor

$\frac{d n}{d t'} = \frac{d n}{d t} \sqrt{\frac{1 - \tanh [θ (t' - x (t_{i}) / c]}{1 + \tanh [θ (t' - x (t_{i}) / c]}}$

(1.9)

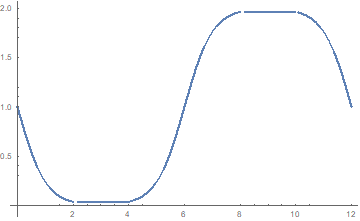
Figure 2: Plot of relative rocket reception rate, dn/dt'/(dn/dt),equation (1.7), as a function of rocket proper time, t, for acceleration=1 light year/year² .