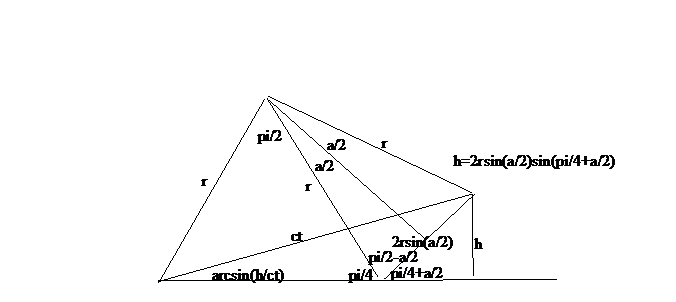Emission Angles of Photons in a Square Ring Resonator

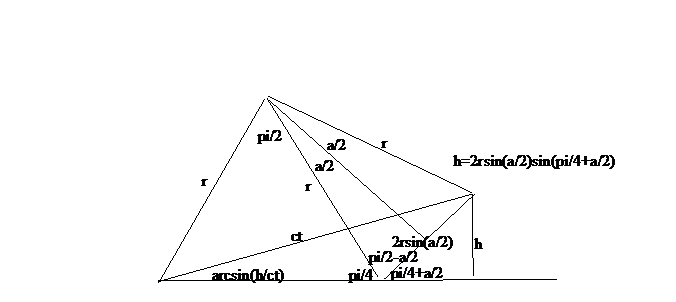
Figure 1: Geometry of mirror center locations, r, after rotation by angle a=wt where w is the rotation rate and t is time.  The angle arcsin(h/ct) is the angle that the particle must be emitted from mirror n to arrive at the center of mirror n+1 when it travels at speed of light c.

 

The equation that must be solved to find the time of traversal from mirror n to mirror n+1 is the following:

f(t)=ct−2r[sin(wt/2+π/4)] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgacaGGOa GaamiDaiaacMcacqGH9aqpcaWGJbGaamiDaiabgkHiTiaaikdacaWG YbGaai4waiGacohacaGGPbGaaiOBaiaacIcacaWG3bGaamiDaiaac+ cacaaIYaGaey4kaSIaeqiWdaNaai4laiaaisdacaGGPaGaaiyxaaaa @4C14@  

(1.1)

This equation is easily solved by the iterative Newton-Raphson method where

t i+1 = t i −f( t i )/f'( t i ) MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadshadaWgaa WcbaGaamyAaiabgUcaRiaaigdaaeqaaOGaeyypa0JaamiDamaaBaaa leaacaWGPbaabeaakiabgkHiTiaadAgacaGGOaGaamiDamaaBaaale aacaWGPbaabeaakiaacMcacaGGVaGaamOzaiaacEcacaGGOaGaamiD amaaBaaaleaacaWGPbaabeaakiaacMcaaaa@47D5@  

(1.2)

where t0 is an initial guess of the actual solution and f' '(t) is the derivative of f with respect to t:

f'(t)=c−2wr[cos(wt/2+π/4)] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgacaGGNa GaaiikaiaadshacaGGPaGaeyypa0Jaam4yaiabgkHiTiaaikdacaWG 3bGaamOCaiaacUfacaGGJbGaai4BaiaacohacaGGOaGaam4Daiaads hacaGGVaGaaGOmaiabgUcaRiabec8aWjaac+cacaaI0aGaaiykaiaa c2faaaa@4CBB@  

(1.3)

An adequate initial guess can be

t≈ 2 r c MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadshacqGHij YUdaWcaaqaamaakaaabaGaaGOmaaWcbeaakiaadkhaaeaacaWGJbaa aaaa@3B65@  

(1.4)

It should be noted that the above calculation works for equilateral  resonators with any number of mirrors, nM, greater than or equal to 3 just by replacing π/4 by π /nM.