Rotor-Rotor Collision Kinetics

1. Similarity to Hard Disc Collisions

Hard disc collisions involve momentum transfers along the lines separating the centers of the two discs of mass m. By Newton's laws, the transfers have to be equal and opposite. For variable mass discs, the momentum transfer to discs 1 and 2 is proportional to

$δ p_{2} = m_{2} δ v_{2} = - m_{1} δ v_{1} \equiv M_{r} δ v c$

(1.1)

where c is a unit vector pointing from the center of disc 1 to the center of disc 2

$c = \frac{r_{1} - r_{2}}{| r_{1} - r_{2} |}$

(1.2)

where the r's are the location vectors of the centers of the discs and M_r is a mass that is still to be determined along with δv.

Energy conservation requires that the energy after the collision is the same as that before the collision.

If v₁and v₂ are the initial velocities of the discs, then the final and initial energies are:

$\frac{1}{2 m_{1}} (m_{1} v_{1} - M_{r} δ v c) • (m_{1} v_{1} - M_{r} δ v c) + \frac{1}{2 m_{2}} (m_{2} v_{2} + M_{r} δ v c) • (m_{2} v_{2} + M_{r} δ v c) = \frac{1}{2} (m_{1} v_{1}^{2} + m_{2} v_{2}^{2})$

$[\frac{M_{r}^{2} δ v^{2}}{2} (\frac{1}{m_{1}} + \frac{1}{m_{2}}) + M_{r} δ v c • (v_{2} - v_{1})] = 0$

(1.3)

Solving for M_rδv we have:

$M_{r} δ v = - 2 c • (v_{2} - v_{1}) \frac{m_{1} m_{2}}{m_{1} + m_{2}}$

(1.4)

Obviously the reduced mass is:

$M_{r} = \frac{2 m_{1} m_{2}}{m_{1} + m_{2}}$

(1.5)

and

$δ v = - c • (v_{2} - v_{1})$

(1.6)

Then:

$\begin{array}{l} v_{2}' = v_{2} - \frac{M_{r}}{m_{2}} c • (v_{2} - v_{1}) \\ v_{1}' = v_{1} + \frac{M_{r}}{m_{1}} c • (v_{2} - v_{1}) \end{array}$

(1.7)

2. Response of a Rotor to an Impulse Applied to One of Its End Masses

The basic driver involved in hard object collisions is an impulse. An impulse is the product of a force times a very small time increment which, of course, leads to a change in momentum like mδv where m is the mass and δv is the change in the velocity. The time increment is small enough that there will be no significant rotation of the rotor or displacement of its center of mass within the duration of the impulse. These motions will occur after the impulse.

The specific diagram for this problem is shown below. To make the problem primitive and simple, both of the initial motions are nil. The final motion will be a combination of a center of mass velocity, δv_x, and a final rotation, at rate δω, about the center of mass. The impulse is along the -x direction as shown.

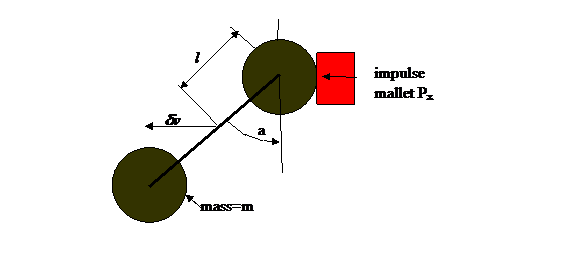
The change in x momentum is a combination of the change in center of mass velocity and rotation speed δω. Here P_x is the impulse F_xdt; Note that P_x is negative.:

$2 (m δ v + m l δ ω \cos a) = P_{x}$

(1.8)

Solving for δω:

$δ ω = \frac{P_{x} - 2 m δ v}{2 m l \cos a}$

(1.9)

The energy supplied by the impulse is F_xdx which is the same as P_x<v_x> where <v_x> is the 1/2 of the final speed that will be obtained by the rotor.

Thus conservation of energy requires that:

$m δ v^{2} + m l^{2} δ ω^{2} = P_{x} \frac{δ v + l δ ω \cos a}{2}$

(1.10)

Inserting the solution for δω:

$m δ v^{2} + m l^{2} {(\frac{P_{x} - 2 m δ v}{2 m l \cos a})}^{2} = P_{x} \frac{δ v + l (\frac{P_{x} - 2 m δ v}{2 m l \cos a}) \cos a}{2} = \frac{P_{x}^{2}}{4 m}$

(1.11)

This is a quadratic equation. Computing a, b, and c coefficients of δv², δv¹, and δv⁰.

$\begin{array}{l} a = m (1 + \frac{1}{\cos^{2} a}) \\ b = - (\frac{P_{x}}{\cos^{2} a}) \\ c = \frac{P_{x}^{2}}{4 m \cos^{2} a} - \frac{P_{x}^{2}}{4 m} \end{array}$

(1.12)

$b^{2} - 4 a c = \frac{P_{x}^{2}}{\cos^{4} a} - P_{x}^{2} (1 + \frac{1}{\cos^{2} a}) (\frac{1}{\cos^{2} a} - 1) = \frac{P_{x}^{2}}{\cos^{4} a} + P_{x}^{2} (1 - \frac{1}{\cos^{4} a}) = P_{x}^{2}$

(1.13)

Solving the quadratic equation for δv we obtain:

$δ v = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} = \frac{\frac{P_{x}}{\cos^{2} a} \pm P_{x}}{2 m (1 + \frac{1}{\cos^{2} a})} = \frac{P_{x}}{2 m}, \frac{P_{x} (1 - \cos^{2} a)}{2 m (1 + \cos^{2} a)}$

(1.14)

The first solution does not allow for the possibility of spin since it gives δω=0. The second solution is more general and is valid for all cases where cos(a) is not equal to zero.

$δ ω = \frac{P_{x} \cos a}{m l (1 + \cos^{2} a)}$

(1.15)

3. Rotor-Disc Collisions

These are similar to hard disc collisions in terms of the momentum transfer. However, the initial and final velocities of each rotor end is a combination of the center of mass (CM) velocities and the rotational velocities. Therefore the momentum changes due to both of these incident velocities have to be equal and opposite to that of the disc and the total energy due to both types of rotor velocity as well as that of the disc has to be the same before and after the collision. For the time being we will limit ourselves to two dimensions (x,y). We can state the r and v vectors in terms of the (x,y) coordinate system and the z axis will be the rotation axis.

$\begin{array}{l} v_{p} = v_{C M} + ω_{} l (- x \sin a_{} + y \cos a_{}) \\ v_{n} = v_{C M} - ω_{} l (- x \sin a_{} + y \cos a_{}) \end{array}$

(1.16)

where subscript p denotes one end (think positive) and n denotes the other end of the rotor, ω is the rotation speed of the rotor, l is half the distance between the rotor ends and a is the angle with respect to the x axis of the rotor's orientation. So the program must check the distances between both the p and the n ends of each rotor and the center of the disc. If this distance is less than or equal to the sum of the radius of the rotor end disc and that of the free disc, then a collision must be calculated. Just as in the case of the hard discs, the momentum transfers must be equal and opposite. However, unlike that case, the momentum transfer to the rotor will be divided into rotational speed changes and velocity changes to the rotor's center of mass.

Figure 1: Illustration of rotor and a disc. The rotor rotational angle with respect to the x axis is a and rotor center of mass velocity v_r The distance between the centers of the rotor end discs is 2l and the radius of the end discs is b_r while the single disc radius is b_d Thus a collision is computed when the distance between disc center and either rotor end center is less than b_r+b_d. u is a unit vector along the length of the rotor, v_ω is a unit vector along the rotational velocity vector of the red end, and c is a unit vector along the line from the center of the disc to the red end of the rotor.

The momentum transfer to the end of the rotor that is hit by the disc is equal and opposite to that transferred to the disc and both magnitudes are equal to an expression M_rδv

The expression for conservation of linear momentum is the following:

$\begin{array}{l} δ p_{d} = - δ p_{r} = - M_{r} δ v c \\ m_{d} δ v_{d} c = - m_{r} δ v_{r} c = - M_{r} δ v c \end{array}$

(1.17)

where the quantity M_rδv will have to be determined by energy conservation and c is a unit vector along the line between centers of the free disc and the colliding end of the rotor disc.

In order to express the conservation of angular momentum, we must define the position of the composite center of mass (CM) including both ends of the rotor and the free disc.

$\begin{array}{l} r_{C M} = \frac{\frac{m_{r}}{2} (r_{p} + r_{n}) + m_{d} r_{d}}{m_{r} + m_{d}} \\ r_{p} = r_{r} + l u_{r}; r_{n} = r_{r} - l u_{r} r_{d} = r_{p} - (b_{r} + b_{d}) c \\ r_{C M} = \frac{m_{r} r_{r} + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \end{array}$

(1.18)

Then the angular momentum with respect to this CM is expressed as:

$\begin{array}{l} L = m_{r} l^{2} ω + m_{r} [(r_{r} - r_{C M}) \times v_{r}] + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c - r_{C M})] \times v_{d} \\ \equiv L_{ω} + L_{v} \end{array}$

(1.19)

and, of course, all terms point along the z axis.

Conservation of angular momentum requires that:

From this equation we can calculate δω

$\begin{array}{l} L_{ω}' + L_{v}' = m_{r} l^{2} (ω + δ ω) + m_{r} [(r_{r} - r_{C M}) \times (v_{r} + δ v_{r})] + m_{d} {[r_{r} + l u_{r} - (b_{r} + b_{d}) c - r_{C M}] \times (v_{d} + δ v_{d})} \\ = m_{r} l^{2} ω + m_{r} [(r_{r} - r_{C M}) \times v_{r}] + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c - r_{C M}] \times v_{d} = L_{ω} + L_{v} \end{array}$ (1.20)

$\begin{array}{l} m_{r} l^{2} (δ ω) + m_{r} [(r_{r} - r_{C M}) \times δ v_{r}] + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c - r_{C M}) \times (δ v_{d})] = 0 \\ δ ω = - \frac{1}{l^{2}} {[(r_{r} - r_{C M}) \times δ v_{r}] - \frac{m_{d}}{m_{r}} [(r_{r} + l u_{r} - (b_{r} + b_{d}) c - r_{C M}) \times δ v_{d}]} = \\ \frac{1}{l^{2}} {[(r_{r} - r_{C M}) \times δ v_{r}] - \frac{m_{d}}{m_{r}} [(r_{d} - r_{C M}) \times δ v_{d}]} \end{array}$

(1.21)

The collision produces a torque impulse equal to

$\begin{array}{l} δ τ = m_{r} δ v_{r} (r_{r} - r_{C M}) \times c - m_{d} δ v_{d} (r_{d} - r_{C M}) \times c = \\ M_{r} δ v_{r} (r_{r} - r_{C M}) \times c δ v - M_{r} δ v (r_{d} - r_{C M}) \times c \end{array}$

(1.22)

Note that r_r-r_CM points in the opposite direction from r_d-r_CM. In fact, we have simple expressions for these vectors:

$\begin{array}{l} r_{r} - r_{C M} = \frac{(m_{r} + m_{d}) r_{r}}{m_{r} + m_{d}} - \frac{m_{r} r_{r} + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} = \\ \frac{- m_{d} [l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \\ r_{d} - r_{C M} = \frac{(m_{r} + m_{d}) [r_{r} + l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} - \frac{m_{r} r_{r} + m_{d} [r_{r} + l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} = \\ \frac{m_{r} [l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \\ r_{r} - r_{C M} - (r_{d} - r_{C M}) = - 2 \frac{m_{d} [l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \end{array}$

(1.23)

$δ τ = - 2 M_{r} δ v \frac{m_{d} [l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \times c$

(1.24)

where M_rδv is computed below. The rotation rate of the rotor has to compensate for this torque in order to conserve angular momentum.

$\begin{array}{l} m_{r} l^{2} δ ω = - δ τ = 2 M_{r} δ v \frac{m_{d} [l u_{r} - (b_{r} + b_{d}) c]}{m_{r} + m_{d}} \times c = 2 M_{r} δ v l \frac{m_{d}}{m_{r} + m_{d}} u_{r} \times c \\ δ ω = 2 \frac{M_{r} δ v}{m_{r} l} \frac{m_{d}}{m_{r} + m_{d}} u_{r} \times c \end{array}$

(1.25)

It should be understood that the orientation (angle a) of the rotor cannot change instantaneously and is therefore the same after the collision as before.

In addition to the momentum conservation, conservation of energy requires that the translational energy before and after the collision be the same and, separately, that the rotational energy about the CM before and after the collision be the same. The reason that translational energy has to be the same is that the velocity, v_CM, of the center of mass cannot change and therefore the product (m_r+m_d)v_CM²/2 can't change. Since the total energy cannot change either, that also means that the rotational energy can't change.

In the following equations I compute the value of the δv in equation 1.17:

$\begin{array}{l} \frac{m_{d}^{2}}{2 m_{d}} (v_{d} - \frac{M_{r} δ v}{m_{d}} c) • (v_{d} - \frac{M_{r} δ v}{m_{d}} c) + \frac{2 m_{r}^{2}}{2 m_{r}} (v_{r} + \frac{M_{r} δ v}{m_{r}} c) • (v_{r} + \frac{M_{r} δ v}{m_{r}} c) = \\ \frac{m_{d}^{2} v_{d}^{2}}{2 m_{d}} + \frac{m_{r}^{2}}{2 m_{r}} (v_{r}) • (v_{r}) \end{array}$

(1.26)

Gathering terms in δv² and δv we have:

$\frac{M_{r}^{2}}{2 m_{d}} δ v^{2} + \frac{M_{r}^{2}}{2 m_{r}} δ v^{2} + M_{r} δ v [- v_{d} • c + (v_{r}) • c] = 0$

(1.27)

$M_{r}^{2} δ v^{2} (\frac{1}{2 m_{d}} + \frac{1}{2 m_{r}}) - M_{r} δ v [v_{d} • c - (v_{r}) • c] = 0$

(1.28)

$M_{r}^{} δ v = \frac{2 m_{d} m_{r}}{m_{d} + m_{r}} [v_{d} • c - v_{r} • c]$

(1.29)

Using this expression in equation 1.17 we have the following values of δv_d and δv_r:

$\begin{array}{l} δ v_{r} = \frac{M_{r} δ v}{m_{r}} = \frac{2 m_{d}}{m_{d} + m_{r}} [v_{d} • c - v_{r} • c] \\ δ v_{d} = - \frac{M_{r} δ v}{m_{d}} = - \frac{2 m_{r}}{m_{d} + m_{r}} [v_{d} • c - v_{r} • c] \end{array}$

(1.30)

which is the same as the expression for hard sphere collisions derived above. Strangely, when the equation 1.31 results are used in equation 1.17 and the latter results are inserted into equation 1.25, we obtain the change in rotation rate without resorting to conservation of angular rotation energy.

$M_{r}^{} δ v = \frac{2 m_{d} m_{r}}{m_{d} + m_{r}} [v_{d} • c - v_{r} • c]$

(1.31)

Our final result for δω is:

$\begin{array}{l} m_{r} l^{2} δ ω = 2 M_{r} δ v l \frac{m_{d}}{m_{r} + m_{d}} u_{r} \times c = 4 l \frac{m_{d}^{2} m_{r}}{{(m_{d} + m_{r})}^{2}} [v_{d} • c - v_{r} • c] (u_{r} \times c) \\ δ ω = 4 \frac{m_{d}^{2}}{{(m_{d} + m_{r})}^{2}} \frac{[v_{d} • c - v_{r} • c]}{l} (u_{r} \times c) \end{array}$

(1.32)

4. Rotor-Rotor Collisions

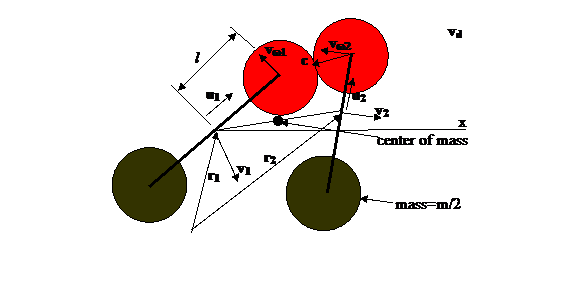
Figure 2: Illustration of 2 rotors colliding . The rotor and center of mass velocity v_CM The distance between the centers of the rotor end discs is 2l and the radius of the end discs is b_r Thus a collision is computed when the distance between disc center and either rotor end center is less than 2b_r. u is a unit vector along the length of the rotor, v_ω is a unit vector along the rotational velocity vector of the red end, and c is a unit vector along the line from the center of one rotor's end disc to the center of the one of the end discs of the other rotor.

Regardless of internal rotation of the rotors, the momentum of the composite center of mass cannot change without some outside force which, in the absence of the walls, we don't have.

$\begin{array}{l} δ p_{1} = - δ p_{2} = M_{r} δ v c \\ m_{1} δ v_{1} = - m_{2} δ v_{2} = M_{r} δ v c \end{array}$

(1.33)

Since the change in momentum can only be along c, we may drop the vectorial notation for δv₁ and δv₂:

$m_{1} δ v_{1} = - m_{2} δ v_{2} = M_{r} δ v$

(1.34)

Conservation of angular momentum requires that the following equation be true:

$\begin{array}{l} l^{2} (m_{1} δ ω_{1} + m_{2} δ ω_{2}) + \frac{1}{2} [m_{1} (2 r_{2} - 2 r_{C M}) \times (δ v_{1}) + m_{2} (2 r_{2} - 2 r_{C M}) \times (δ v_{2})] \\ m_{1} δ ω_{1} + m_{2} δ ω_{2} = - \frac{1}{l^{2}} [m_{1} (r_{1} - r_{C M}) \times (δ v_{1}) + m_{2} (r_{2} - r_{C M}) \times (δ v_{2})] \equiv f (δ v) \end{array}$

(1.35)

Therefore δω₁ can be calculated as:

$δ ω_{1} = - \frac{1}{m_{1}} {f (δ v) - m_{2} δ ω_{2}}$

(1.36)

Since either rotor 1 or rotor 2 could change rotation speed to compensate for the torque impulse induced by the collision, I also need to invoke conservation of rotational energy to compute δω₂.

The energy associated with angular momentum is the same before and after the collision

$\begin{array}{l} E_{L}' = \frac{1}{2} l^{2} (m_{1} ω_{1}^{2} + m_{2} ω_{2}^{2} + 2 m_{1} ω_{1} δ ω_{1} + 2 m_{2} ω_{2} δ ω_{2} + m_{1} δ ω_{1}^{2} + m_{2} δ ω_{2}^{2}) + \\ \frac{1}{2} [m_{1} \frac{| v_{1} + δ v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times (v_{1} + δ v_{1}) + m_{2} \frac{| v_{2} + δ v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times (v_{2} + δ v_{2})] = \\ \frac{1}{2} l^{2} (m_{1} ω_{1}^{2} + m_{2} ω_{2}^{2}) + m_{1} \frac{| v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times (v_{1}) + m_{2} \frac{| v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times (v_{2}) = E_{L} \end{array}$

(1.37)

Therefore we have the following equation from which to obtain ω₂:

$\begin{array}{l} \frac{1}{2} l^{2} (- 2 ω_{1} {f (δ v) - m_{2} δ ω_{2}} + 2 m_{2} ω_{2} δ ω_{2} + \frac{1}{m_{1}} {f (δ v) - m_{2} δ ω_{2}}^{2} + m_{2} δ ω_{2}^{2}) + \\ \frac{1}{2} [m_{1} \frac{| v_{1} + δ v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times (v_{1} + δ v_{1}) + m_{2} \frac{| v_{2} + δ v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times (v_{2} + δ v_{2})] - \\ m_{1} \frac{| v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times v_{1} + m_{2} \frac{| v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times v_{2} = 0 \end{array}$

(1.38)

This equation is of the form A δω₂² +Bδω₂+C where the coefficients are:

$\begin{array}{l} A = \frac{m_{2} l^{2}}{2} (1 + \frac{m_{2}^{}}{m_{1}}) \\ B = m_{2} l^{2} [ω_{2} - ω_{1} - \frac{m_{2}^{}}{m_{1}} f (δ v)] \\ C = \frac{1}{2} [l^{2} (- 2 ω_{1} {f (δ v)} + \frac{1}{m_{1}} {f (δ v)}^{2}) + m_{1} \frac{| v_{1} + δ v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times (v_{1} + δ v_{1}) + m_{2} \frac{| v_{2} + δ v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times (v_{2} + δ v_{2})] - \\ [m_{1} \frac{| v_{1} |}{| r_{1} - r_{C M} |} (r_{1} - r_{C M}) \times v_{1} + m_{2} \frac{| v_{2} |}{| r_{2} - r_{C M} |} (r_{2} - r_{C M}) \times v_{2}] \end{array}$ (1.39)

The solution for δω₂ is then:

$δ ω_{2} = \frac{- B \pm \sqrt{B^{2} - 4 A C}}{2 A}$

(1.40)

Using this latter result will conserve both linear and angular momentum and energy.