Gravity Assist Animation

Introduction

Propellant for probes to other planets in our solar system can be greatly reduced by use of close flybys of planets. The main reason for this is that the planet has a lot of orbital speed so that, when the spacecraft is under its gravitational force influence, the planet tends to make a component of the spacecraft's velocity equal to its own orbital speed. This effect is explored by this animation.

y

Figures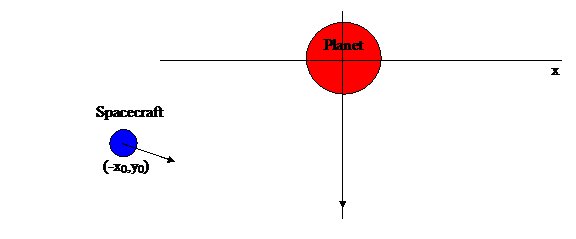

Figure 1:Diagram of the initial positions of the spacecraft and the planet. In order to provide energy to the spacecraft, the planet has more speed than the spacecraft.

Figure 2: Diagram of the animation showing closest approach of spacecraft to planet under influence of gravity attraction.

Math for Computing Starting Conditions for Close Intercept

We will assume the planet starts at y=0 and is moving downward at speed vyp along the y axis. The spacecraft, at the start, is poised farther down at -y₀ and in the x direction at -x₀ from the y axis where both x₀ and y₀ are positive numbers. The initial velocity of the spacecraft will be (v_x0,v_y0). We need to be able to compute the appropriate distance x₀ from the y axis for the start position of the spacecraft. Without any change in speed, the time required for the spacecraft to cross the y axis is

$t = \frac{y_{0}}{v_{p y} - v_{y 0}}$

(1.1)

For the spacecraft to intercept the planet which is on the y axis we must then set a nominal value for x0 to be

$x_{0} = t_{int} v_{x 0}$

(1.2)

The above values of the starting position for the spacecraft would cause the intercept to occur at the center of planet.

We want to have the intercept occur with an offset, s_o, from the rim of the planet. If the radius of the planet is a, then the distance from the planet center is d_int=a+s_o. A unit vector along the normal to the relative velocity vector can be written in terms of the differential velocities:

$\begin{array}{l} d v_{x} = v_{x 0} \\ d v_{y} = v_{p y} - v_{y 0} \end{array}$

(1.3)

Then the normal n_dvto the relative velocity vector can be written:

$\begin{array}{l} d v_{a b s} = \sqrt{d v_{x} d v_{x} + d v_{y} d v_{y}} \\ n_{d v} = \frac{- d v_{y}}{d v_{a b s}} x + \frac{d v_{x}}{d v_{a b s}} y \end{array}$

(1.4)

To correct both x₀ and y₀for the offset and the radius of the planet we need to use this normal vector:

$\begin{array}{l} x_{0}^{'} = x_{0} + d_{int} n_{d v}_{x} \\ y_{0}^{'} = y_{0} + d_{int} n_{d v}_{y} \end{array}$

(1.5)

Effect of Gravity on Closest Approach

Obviously the slower the relative starting speed, the more the effect of gravity on the final intercept distance. And the approach speed is constantly changing due to gravity. At any center to center distance r, the acceleration, , due to gravity is

$a = \frac{G M}{r^{3}} (d x x + d y y) = \frac{G M}{| r_{p} - r_{s} |^{3}} (r_{p} - r_{s})$

(1.6)

where

$\begin{array}{l} d x = x_{p} - x_{s} \\ d y = y_{p} - y_{s} \\ r = \sqrt{d x^{2} + d y^{2}} \end{array}$

(1.7)

Obviously the speed at any position $(x_{s}, y_{s})$ will be affected by the acceleration:

$\frac{d v_{s}}{d t} = a$

(1.8)

and further the position will be influenced by this speed change:

$r_{s} (t) = r_{s} (0) + v_{0} t + G M \int_{t'}^{t} d t' \int_{0}^{t'} \frac{r_{p} - r_{s}}{| r_{p} - r_{s} |^{3}} d t''$

(1.9)

A more acceptable form of this equation has r_p-r_s as the variable:

$r_{p} - r_{s} = r_{p} (0) - r_{s} (0) + (v_{p} - v_{s} (0)) t + G M \int_{t'}^{t} d t' \int_{0}^{t'} \frac{r_{p} - r_{s}}{| r_{p} - r_{s} |^{3}} d t''$

(1.10)

It is probably best to solve this equation for r_s(t) numerically and provide the results to the learner.

Energy Required for Course Correction After Gravity Assist

The spacecraft direction, arctangent(vy/vx), is changed by gravity assist and it is important to consider how much energy is required to correct the course. We can always make this correction long after the gravity assist by applying force in the direction normal to the present course. The unit normal vector, n_v, to the spacecraft direction is given by:

$n_{v} = \frac{- v_{y} x + v_{x} y}{\sqrt{v_{x}^{2} + v_{y}^{2}}}$

(1.11)

We want to apply acceleration along this normal vector until

_{$\frac{v_{y}}{v_{x}} = \frac{v_{y 0}}{v_{x 0}}$}

_(1.12)

The power needed to cause this acceleration is

$P = F • v = m a n_{v} • v$

(1.13)

where F is the force, m is the mass of the spacecraft and a is the magnitude of the acceleration. Using equation (1.11) in equation 113 we have

$P = m a (\frac{- v_{y} x + v_{x} y}{\sqrt{v_{x}^{2} + v_{y}^{2}}}) • (v_{x} x + v_{y} y) = m a \frac{(- v_{x} v_{y} + v_{x} v_{y})}{\sqrt{v_{x}^{2} + v_{y}^{2}}} = 0$

(1.14)

So the power needed is identically zero as long at the acceleration is normal to the current velocity. That also means that the energy needed is identically zero. The reason for this strange result is that, if a particle's velocity is zero, then it requires only infinitesimal energy input to change the velocity by a small amount i.e. E_in=mvdv=0 when v is zero. A physical analogy for this behavior is that of a charged particle that has a magnetic field applied normal to the plane of the particle's trajectory. If the field is applied for a very short time, the path of the particle will be an arc of constant radius. As is well known, the particle will not change its kinetic energy due to the magnetic field. The above result assumes that the spacecraft has left the influence of the gravity on the planet.

Introduction

y Figures

Math for Computing Starting Conditions for Close Intercept

Effect of Gravity on Closest Approach

Energy Required for Course Correction After Gravity Assist

y

Figures