Convex Lens Best Focus Distance

Calculations

In the limit where the radial displacement, r, is much less than the radius of curvature, R, we will find the distance, f, where the total optical phase path is independent of r.

Figures

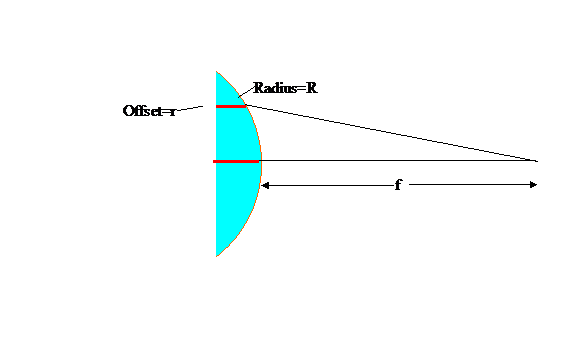
Figure 1: The red rays are inside the lens while the black rays are in air. Therefore the optical path length for the red rays is their lengths multiplied by the index of refraction of the lens while the optical path length for the blach rays us just their lengths.

The difference in path lengths for the rays in the lens is

$s (0) - s (r) \equiv δ s_{l e n s} = R - \sqrt{R^{2} - r^{2}}$

(0.1)

The difference in the starting x coordinate between the air ray a the lens center and the air ray at the r location of the lens is also $δ s_{l e n s}$

Therefore the difference in lengths of the air rays is

$s_{a i r} (r) - s_{a i r} (0) = \sqrt{{(f + δ s_{l e n s})}^{2} + r^{2}} - f$

(0.2)

The difference in optical path length can now be written:

$\begin{array}{l} p (r) - p (0) = s (r) - s (0) - n \sqrt{R^{2} - r^{2}} \\ = \sqrt{{(f + R - \sqrt{R^{2} - r^{2}})}^{2} + r^{2}} - (f + n (R - \sqrt{R^{2} - r^{2}})) \end{array}$

(0.3)

Now, if the reader can bear with me I will show that f>>r just if R>r so I may expand the square roots to first order in a Taylor series.

The expression for ds_lens expands to:

$δ s_{l e n s} \approx \frac{r^{2}}{2 R}$

(0.4)

so that the optical path difference can now be written:

$p (r) - p (0) \approx \sqrt{{(f + \frac{r^{2}}{2 R})}^{2} + r^{2}} - (f + n \frac{r^{2}}{2 R})$

(0.5)

Since f>>r we can now expand the square root term to yield:

$\begin{array}{l} p (r) - p (0) \approx f \sqrt{{(1 + \frac{r^{2}}{2 f R})}^{2} + \frac{r^{2}}{f^{2}}} - (f + n \frac{r^{2}}{2 R}) \\ \approx f \sqrt{1 + \frac{2 r^{2}}{2 f R} + \frac{r^{2}}{f^{2}}} - (f + n \frac{r^{2}}{2 R}) \\ \approx f + \frac{r^{2}}{2 R} + \frac{r^{2}}{2 f} - (f + n \frac{r^{2}}{2 R}) = r^{2} (\frac{1}{2 f} + \frac{1}{2 R} - \frac{n}{2 R}) = 0 \end{array}$

(0.6)

If r is not zero then we have the equation:

$\begin{array}{l} \frac{1}{f} + \frac{1}{R} - \frac{n}{R} = 0 \\ f = \frac{R}{n - 1} \end{array}$

(0.7)